Published: Sun 25 October 2015
Updated: Wed 18 November 2015
By Tingran Gao
In Math 212 .
tags: Math 212 Quiz
Problem 1. Compute each of the following volumes enclosed by two surfaces.
(a) The sphere \(x^2+y^2+z^2=a^2\) and cylinder \(x^2+y^2=ax\) ;
(b) The cone \(z=\sqrt{x^2+y^2}\) and the cylinder \(z^2=2x\) ;
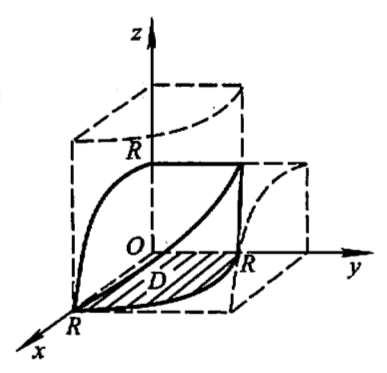
(c) The two cylinders \(x^2+y^2=R^2\) and \(x^2+z^2=R^2\) .
Problem 2. Find the center of mass of the following plane regions.
(a) \(D\) enclosed by \(y=\sqrt{2px}, \,\, x=x_0>0, \,\, y=0\) ;
(b) \(D\) is the semi-ellipse \(\left\{\left(x,y\right)\mid \frac{x^2}{a^2}+\frac{y^2}{b^2}\leq 1, y\geq 0 \right\}\) ;
(b) \(D\) enclosed by two disks \(\rho=a\cos\theta\) and \(\rho=b\cos\theta\) (\(0<a<b\) , \(-\frac{\pi}{2}\leq \theta\leq \frac{\pi}{2})\) .
Problem 3. Find the center of mass of the plane region \(D\) enclosed by \(y=x^2\) and \(y=x\) , with density function
$$\mu \left(x,y\right) = x^2y.$$
Problem 4. Compute the center of mass of the following solid bodies (using triple integrals, of course). Assume the density is identically equal to \(1\) .
(a) \(\Omega\) enclosed by \(z^2=x^2+y^2\) and \(z=1\) ;
(b) \(\Omega\) enclosed by \(z=\sqrt{A^2-x^2-y^2}\) , \(z=\sqrt{a^2-x^2-y^2}\) , and \(z=0\) (assuming \(A>a>0\) );
(c) \(\Omega\) enclosed by \(z=x^2+y^2\) , \(x+y=a\) , \(x=0\) , \(y=0\) , \(z=0\) .
Problem 5. Compute the moments of inertia \(I_x\) , \(I_y\) , \(I_0\) for the following plane regions.
(a) \(D=\left\{\left(x,y\right)\mid \frac{x^2}{a^2}+\frac{y^2}{b^2}\leq 1\right\}\) ;
(b) \(D\) enclosed by \(y^2=\frac{9}{2}x\) and \(x=2\) ;
(c) \(D\) is the rectangle \(\left[0,a\right]\times\left[0,b\right]\) .
Problem 6. Consider the solid body \(\Omega\) (with constant density \(\rho_0\) ) enclosed by the surface \(z=x^2+y^2\) , \(z=0\) , \(\left|x\right|=a, \left|y\right|=a\) . Compute:
(1) The volume of \(\Omega\) ;
(2) The center of mass of \(\Omega\) ;
(3) The moment of inertia of \(\Omega\) with respect to the \(z\) axis.
Problem 7. Find the moment of inertial of a cylinder with respect to its axis of symmetry, assuming the height of the cylinder is \(h\) , the radius of its base is \(a\) , and the density is identically equal to \(1\) .
Problem 8. Use triple integral to compute the volume of the unit ball \(\left\{\left(x,y,z\right)\mid x^2+y^2+z^2\leq 1\right\}\) .
Answers
Problem 1.
(a) \(\frac{2}{3}a^3\left(\pi-\frac{4}{3}\right)\) \(\qquad\) (b) \(2\pi-\frac{32}{9}\) \(\qquad\) (c) \(\frac{16}{3}R^3\)
Problem 2.
(a) \(\bar{x} = \frac{3}{5}x_0\) , \(\bar{y}=\frac{3}{8}\sqrt{2px_0}\) . \(\quad\) (b) \(\bar{x}=0\) , \(\bar{y}=\frac{4b}{3\pi}\) . \(\quad\) (c) \(\bar{x}=\frac{a^2+ab+b^2}{2\left(a+b\right)}\) , \(\bar{y}=0\) .
Problem 3.
\(\bar{x} = \frac{35}{48}\) , \(\bar{y} = \frac{35}{54}\) .
Problem 4.
(a) \(\left(0,0,\frac{3}{4}\right)\) \(\quad\) (b) \(\left(0,0,\frac{3\left(A^4-^4\right)}{8\left(A^3-a^3\right)}\right)\) \(\quad\) (c) \(\left(\frac{2}{5}a, \frac{2}{5}a, \frac{7}{30}a^2\right)\)
Problem 5.
(a) \(I_x = \frac{1}{4}\pi ab^3\) , \(I_y = \frac{1}{4}\pi a^3b\) \(\quad\) (b) \(I_x = \frac{72}{5}\) , \(I_y=\frac{96}{7}\) \(\quad\) (c) \(I_x=\frac{1}{3}ab^3\) , \(I_y=\frac{1}{3}a^3b\)
Problem 6.
(1) \(\frac{8}{3}a^4\) \(\quad\) (2) \(\bar{x}=\bar{y}=0,\,\, \bar{z}=\frac{7}{15}a^2\) \(\quad\) (3) \(\frac{112}{45}a^6\rho_0\)
Problem 7.
\(\frac{\pi}{2}a^4h\)
Problem 8.
\(\frac{4}{3}\pi\)
Solutions to Selected Problems
Problem 1 (a). The volume is bounded by two graphs \(z_\mathrm{top}=\sqrt{a^2-x^2-y^2}\) and \(z_\mathrm{bottom}=-\sqrt{a^2-x^2-y^2}\) over the region \(x^2+y^2=ax\) . The volume is thus equal to the double integral
\begin{align*}
&\iint_{\left\{\left(x,y\right)\mid x^2+y^2-ax\leq 0\right\}}\left[\sqrt{a^2-x^2-y^2}-\left(-\sqrt{a^2-x^2-y^2}\right)\right]dA\\
&=\iint_{\left\{\left(x,y\right)\mid x^2+y^2-ax\leq 0\right\}}2\sqrt{a^2-x^2-y^2}\,dA
\end{align*}
Note that the region defined by \(x^2+y^2-ax\leq 0\) can be written in polar coordinates as \(r\leq a\cos\theta\) , with \(\theta\) ranging from \(-\frac{\pi}{2}\) to \(\frac{\pi}{2}\) . Thus the above integral equals
\begin{align*}
\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_0^{a\cos\theta}2\sqrt{a^2-r^2}\,rdr\,d\theta.
\end{align*}
The inner integral can be computed via a substitution \(u=r^2\) :
\begin{align*}
&\int_0^{a\cos\theta}2\sqrt{a^2-r^2}\,rdr=\int_0^{a^2\cos^2\theta}\sqrt{a^2-u}\,du\\
&=-\frac{2}{3}\left(a^2-u\right)^{\frac{3}{2}}\Bigg|_{u=0}^{u=a^2\cos^2\theta}=-\frac{2}{3}a^3\sin^3\theta+\frac{2}{3}a^3=\frac{2}{3}a^3\left(1-\sin^3\theta\right).
\end{align*}
Plug this back into the outer integral, one has
\begin{align*}
\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{2}{3}a^3\left(1-\sin^3\theta\right)\,d\theta&=\frac{2}{3}a^3\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(1-\sin^3\theta\right)\,d\theta\\
&=\frac{2}{3}a^3\left(\pi-\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin^3\theta\,d\theta\right)=\frac{2}{3}a^3\left(\pi-\frac{4}{3}\right).
\end{align*}
The computation of the last integral involving \(\sin^3\theta\) is standard (see page TA-3 in the textbook). It can be done as follows:
\begin{align*}
\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin^3\theta\,d\theta &= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin^2\theta\cdot\sin\theta\,d\theta\\
&=-\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(1-\cos^2\theta\right)d\cos\theta=-2\int_{0}^{\frac{\pi}{2}}\left(1-\cos^2\theta\right)d\cos\theta\\
&\stackrel{t=\cos\theta}{=\!=\!=\!=\!=\!=}-2\int_1^0\left(1-t^2\right)dt=2\int_0^1\left(1-t^2\right)dt=2\left(1-\frac{2}{3}\right)=\frac{4}{3}.
\end{align*}
Problem 1 (b). The volume is bounded by two graphs \(z_\mathrm{top}=2x\) and \(z_\mathrm{bottom}=\sqrt{x^2+y^2}\) over the region \(x^2+y^2-2x\leq 0\) . (The boundary of the region, which is \(x^2+y^2-2x=0\) , can be determined by computing the intersection of \(z=\sqrt{x^2+y^2}\) and \(z^2=2x\) .) Similar to Problem 1 (a), this region can be represented in polar coordinates as \(r\leq 2\cos\theta\) with \(\theta\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\) . The volume can thus be computed as
\begin{align*}
&\iint_{\left\{\left(x,y\right)\mid x^2+y^2-2x\leq 0\right\}}\left[2x-\sqrt{x^2+y^2}\right]dA=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_0^{2\cos\theta}\left(2r\cos\theta-r\right)\,rdr\,d\theta\\
=&\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(2\cos\theta-1\right)\int_0^{2\cos\theta}r^2dr\,d\theta=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(2\cos\theta-1\right)\cdot\frac{8}{3}\cos^3\theta\,d\theta\\
=&\frac{16}{3}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^4\theta\,d\theta-\frac{8}{3}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^3\theta\,d\theta=\frac{16}{3}\times \frac{3\pi}{8}-\frac{8}{3}\times \frac{4}{3}=2\pi-\frac{32}{9}.
\end{align*}
The integrals involving \(\cos^3\theta\) and \(\cos^4\theta\) can be found on page TA-3 in the textbook, or computed as follows:
\begin{align*}
\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^3\theta\,d\theta&=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^2\theta\,d\sin\theta\stackrel{u=\cos\theta}{=\!=\!=\!=\!=\!=}\int_{-1}^1\left(1-u^2\right)du=2-\frac{2}{3}=\frac{4}{3},\\
\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^4\theta\,d\theta&=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^3\theta\,d\sin\theta=\sin\theta\cos^3\theta\Bigg|_{\theta=-\frac{\pi}{2}}^{\theta=\frac{\pi}{2}}-\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin\theta\,d\cos^3\theta\\
&=0-\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin\theta\cdot 3\cos^2\theta \left(-\sin\theta\right)\,d\theta\\
&=3\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin^2\theta \cos^2\theta \,d\theta=\frac{3}{4}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(2\sin\theta\cos\theta\right)^2d\theta\\
&=\frac{3}{4}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin^2 2\theta\,d\theta=\frac{3}{4}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1-\cos 4\theta}{2}d\theta\\
&=\frac{3}{4}\left(\frac{\pi}{2}-\frac{1}{2}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos 4\theta\,d\theta\right)\\
&=\frac{3}{4}\left(\frac{\pi}{2}-\frac{1}{2}\times\frac{1}{4}\sin 4\theta\Bigg|_{\theta = -\frac{\pi}{2}}^{\theta=\frac{\pi}{2}}\right)=\frac{3}{4}\times\frac{\pi}{2}=\frac{3\pi}{8}.
\end{align*}
Problem 1 (c). The volume is two graphs \(z_\mathrm{top}=\sqrt{R^2-x^2}\) and \(z_\mathrm{bottom}=-\sqrt{R^2-x^2}\) over the (disk of radius \(R\) ) region \(x^2+y^2\leq R^2\) . Thus the desired volume is
\begin{align*}
&\iint_{\left\{\left(x,y\right)\mid x^2+y^2\leq R^2\right\}}\left[\sqrt{R^2-x^2}-\left(-\sqrt{R^2-x^2}\right)\right]dA=\iint_{\left\{\left(x,y\right)\mid x^2+y^2\leq R^2\right\}}2\sqrt{R^2-x^2}\,dA\\
=&\int_0^{2\pi}\!\!\!\int_0^R 2\sqrt{R^2-r^2\cos^2\theta}\,\,rdr\,d\theta=\int_0^{2\pi}\!\!\!\int_0^R \sqrt{R^2-r^2\cos^2\theta}\,\,d\left(r^2\right)\,d\theta\\
=&4\int_0^{\frac{\pi}{2}}\!\!\!\int_0^R \sqrt{R^2-r^2\cos^2\theta}\,\,d\left(r^2\right)\,d\theta\\
&\!\!\!\!\stackrel{u=r^2}{=\!=\!=\!=\!=\!=}4\int_0^{\frac{\pi}{2}}\!\!\!\int_0^{R^2}\sqrt{R^2-u\cos^2\theta}\,\,du\,d\theta=4\int_0^{\frac{\pi}{2}}-\frac{2}{3\cos^2\theta}\left(R^2-u\cos^2\theta\right)^{\frac{3}{2}}\Bigg|_{u=0}^{u=R^2}\,d\theta\\
=&4\int_0^{\frac{\pi}{2}}\frac{2}{3\cos^2\theta}R^3-\frac{2}{3\cos^2\theta}\left(R^2-R^2\cos^2\theta\right)^{\frac{3}{2}}d\theta=4\int_0^{\frac{\pi}{2}}\frac{2R^3}{3\cos^2\theta}\left(1-\sin^3\theta\right)\,d\theta\\
=&\frac{8R^3}{3}\int_0^{\frac{\pi}{2}}\frac{1-\sin^3\theta}{\cos^2\theta}\,d\theta=\frac{16R^3}{3}.
\end{align*}
Note that the last step follows from the following computation
\begin{align*}
&\int_0^{\frac{\pi}{2}}\frac{1-\sin^3\theta}{\cos^2\theta}\,d\theta=\int_0^{\frac{\pi}{2}}\frac{\left(1-\sin\theta\right)\left(1+\sin\theta+\sin^2\theta\right)}{1-\sin^2\theta}\,d\theta\\
=&\int_0^{\frac{\pi}{2}}\frac{\left(1-\sin\theta\right)\left(1+\sin\theta+\sin^2\theta\right)}{\left(1-\sin\theta\right)\left(1+\sin\theta\right)}\,d\theta\\
=&\int_0^{\frac{\pi}{2}}\frac{1+\sin\theta+\sin^2\theta}{1+\sin\theta}\,d\theta=\int_0^{\frac{\pi}{2}}\frac{1+\sin\theta\left(1+\sin\theta\right)}{1+\sin\theta}\,d\theta\\
=&\int_0^{\frac{\pi}{2}}\frac{d\theta}{1+\sin\theta}+\int_0^{\frac{\pi}{2}}\sin\theta\,d\theta=\int_0^{\frac{\pi}{2}}\frac{d\theta}{1+\sin\theta}+1\\
=&\int_0^{\frac{\pi}{2}}\frac{d\theta}{1+2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}+1\\
=&\int_0^{\frac{\pi}{2}}\frac{d\theta}{\sin^2\frac{\theta}{2}+\cos^2\frac{\theta}{2}+2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}+1\\
=&\int_0^{\frac{\pi}{2}}\frac{d\theta}{\left(\sin\frac{\theta}{2}+\cos\frac{\theta}{2}\right)^2}+1\\
=&\int_0^{\frac{\pi}{2}}\frac{d\theta}{\cos^2\frac{\theta}{2}\left(\tan\frac{\theta}{2}+1\right)^2}+1\\
=&\int_0^{\frac{\pi}{2}}\frac{d\left(2\tan\frac{\theta}{2}\right)}{\left(\tan\frac{\theta}{2}+1\right)^2}+1\qquad\textrm{becase $\frac{d}{d\theta}\tan\frac{\theta}{2}=\frac{1}{2\cos^2\frac{\theta}{2}}$}\\
&\!\!\!\!\stackrel{u=tan\frac{\theta}{2}}{=\!=\!=\!=\!=\!=}\int_0^{1}\frac{2du}{\left(u+1\right)^2}\,d\theta+1=-\frac{2}{u+1}\Bigg|_{u=0}^{u=1}+1=-1+2+1=2.
\end{align*}
The region enclosd by two cylinders of equal radii is a highly interesting object in geometry and goes a long way back in the pre-history of calculus. Check this article from Wolfram MathWorld and this page from TAMU for more details.
Problem 2 (a). By definition,
\begin{align*}
m&=\iint_D\,dx\,dy=\int_0^{x_0}\!\!\!\int_0^{\sqrt{2px}}dy\,dx=\int_0^{x_0}\sqrt{2px}\,dx=\frac{2}{3}\sqrt{2px_0^3},\\
\bar{x}&=\frac{1}{m}\iint_Dx\,dx\,dy=\frac{1}{m}\int_0^{x_0}\!\!\!\int_0^{\sqrt{2px}}x\,dy\,dx=\frac{1}{m}\int_0^{x_0}\sqrt{2px^3}\,dx\\
&=\frac{3}{2\sqrt{2px_0^3}}\cdot\frac{2}{5}\sqrt{2px_0^5}=\frac{3}{5}x_0,\\
\bar{y}&=\frac{1}{m}\iint_Dy\,dx\,dy=\frac{1}{m}\int_0^{x_0}\!\!\!\int_0^{\sqrt{2px}}y\,dy\,dx=\frac{1}{m}\int_0^{x_0}\frac{1}{2}\cdot 2px\,dx\\
&=\frac{3}{2\sqrt{2px_0^3}}\cdot\frac{1}{2}px_0^2=\frac{3}{8}\sqrt{2px_0}.
\end{align*}
Problem 3. By definition,
\begin{align*}
m&=\iint_Dx^2y\,dA=\int_0^1\!\!\!\int_{x^2}^xx^2y\,dy\,dx=\int_0^1\frac{x^2}{2}\left(x^2-x^4\right)\,dx\\
&=\left(\frac{x^5}{10}-\frac{x^7}{14}\right)\Bigg|_{x=0}^{x=1}=\frac{1}{10}-\frac{1}{14}=\frac{1}{35},\\
\bar{x}&=\frac{1}{m}\iint_Dx\cdot x^2y\,dA=35\int_0^1\!\!\!\int_{x^2}^xx^3y\,dy\,dx=35\int_0^1\frac{x^3}{2}\left(x^2-x^4\right)\,dx\\
&=\frac{35}{2}\left(\frac{x^6}{6}-\frac{x^8}{8}\right)\Bigg|_{x=0}^{x=1}=\frac{35}{2}\cdot\frac{1}{24}=\frac{35}{48},\\
\bar{y}&=\frac{1}{m}\iint_Dy\cdot x^2y\,dA=35\int_0^1\!\!\!\int_{x^2}^xx^2y^2\,dy\,dx=35\int_0^1\frac{x^2}{3}\left(x^3-x^6\right)\,dx\\
&=\frac{35}{3}\left(\frac{x^6}{6}-\frac{x^9}{9}\right)\Bigg|_{x=0}^{x=1}=\frac{35}{3}\cdot\frac{3}{54}=\frac{35}{54}.
\end{align*}
Problem 4 (a). By symmetry, \(\bar{x}=0\) , \(\bar{y}=0\) . The total mass is (note that the density is identically \(1\) )
\begin{align*}
m&=\iiint_\Omega dV=\int_0^1\iint_{\left\{\left(x,y\right)\mid x^2+y^2\leq z^2\right\}}\,dA\,dz\\
&=\int_0^1\pi z^2\,dz=\frac{\pi}{3}z^3\Bigg|_{z=0}^{z=1}=\frac{\pi}{3},
\end{align*}
thus the \(z\) -coordinate of the center of mass is
\begin{align*}
\bar{z}&=\frac{1}{m}\iiint_\Omega z\,dV=\frac{3}{\pi}\int_0^1\iint_{\left\{\left(x,y\right)\mid x^2+y^2\leq z^2\right\}}z\,dA\,dz\\
&=\frac{3}{\pi}\int_0^1\pi z^2\cdot z\,dz=\frac{3}{\pi}\cdot\frac{\pi}{4}z^4\Bigg|_{z=0}^{z=1}=\frac{3}{4}.
\end{align*}
Problem 5 (a). Direct computation gives
\begin{align*}
I_y&=\iint_D x^2\,dA=\int_{-a}^a\!\!\!\int_{-\frac{b}{a}\sqrt{a^2-x^2}}^{\frac{b}{a}\sqrt{a^2-x^2}}x^2\,dy\,dx\\
&=\frac{2b}{a}\int_{-a}^ax^2\sqrt{a^2-x^2}\,dx=\frac{4b}{a}\int_{0}^ax^2\sqrt{a^2-x^2}\,dx\\
&\stackrel{x=\sin\theta}{=\!=\!=\!=\!=\!=}\frac{4b}{a}\int_{0}^{\frac{\pi}{2}}a^3\sin^2\theta\cos\theta\cdot a\cos\theta\,d\theta\\
&=4a^3b\int_{0}^{\frac{\pi}{2}}\left(\sin^2\theta\left(1-\sin^2\theta\right)\right)\,d\theta\\
&=4a^3b\left[\int_{0}^{\frac{\pi}{2}}\sin^2\theta\,d\theta-\int_{0}^{2\pi}\sin^4\theta\,d\theta\right]\\
&=4a^3b\left(\frac{\pi}{4}-\frac{3\pi}{8}\right)=\frac{1}{4}\pi a^3b.
\end{align*}
(The integral involving \(\sin^4\theta\) is computed using the same idea as that used for integrating \(\cos^4\theta\) in the solution to Problem 1 (b).)
By symmetry, \(I_x=\frac{1}{4}\pi ab^3\) . Thus
$$I_0=I_x+I_y=\frac{\pi}{4}ab\left(a^2+b^2\right).$$
Problem 6. Take a look at the graph of the function \(z=x^2+y^2\) , as follows. (Rotate/Zoom with mouse.)
(1) The volume of \(\Omega\) equals to the volume under the graph \(z=x^2+y^2\) over the rectangle bounded by \(\left|x\right|\leq a\) , \(\left|y\right|\leq a\) . Thus
\begin{align*}
\mathrm{Vol}\left(\Omega\right)&=\iint_{\left\{\left(x,y\right)\mid \left|x\right|\leq a, \left|y\right|\leq a\right\}}\left(x^2+y^2\right)\,dA\\
&=\int_{-a}^a\int_{-a}^a\left(x^2+y^2\right)\,dx\,dy\\
&=\int_{-a}^a \left(\frac{1}{3}x^3+xy^2\right)\Bigg|_{x=-a}^{x=a} \,dy\\
&=\int_{-a}^a\left(\frac{2}{3}a^3+2ay^2\right)\,dy\\
&=\frac{2}{3}a^3\cdot 2a+2a\cdot \frac{2}{3}a^3=\frac{8}{3}a^4.
\end{align*}
(2) Since the density of \(\Omega\) is constant \(\rho_0\) , the total mass is
$$m=\rho_0\cdot\mathrm{Vol}\left(\Omega\right)=\frac{8}{3}a^4\rho_0$$
The \(z\) -coordinate of the center of mass is thus
\begin{align*}
\bar{z}&=\frac{1}{m}\iiint_{\Omega}\rho_0 z\,dV=\frac{1}{m}\int_{-a}^a\!\!\int_{-a}^a\!\!\int_0^{x^2+y^2}\rho_0 z\,dz\,dy\,dx\\
&=\frac{\rho_0}{m}\int_{-a}^a\!\!\int_{-a}^a\frac{1}{2}\left(x^2+y^2\right)^2\,dy\,dx\\
&=\frac{\rho_0}{2m}\int_{-a}^a\!\!\int_{-a}^a\left(x^4+2x^2y^2+y^4\right)\,dy\,dx\\
&=\frac{\rho_0}{2m}\int_{-a}^a\left(x^4y+\frac{2}{3}x^2y^3+\frac{1}{5}y^5\right)\Bigg|_{y=-a}^{y=a}dx\\
&=\frac{\rho_0}{2m}\int_{-a}^a\left(2ax^4+\frac{4a^3}{3}x^2+\frac{2a^5}{5}\right)\,dx\\
&=\frac{\rho_0}{2m}\left(2a\cdot\frac{1}{5}x^5+\frac{4a^3}{3}\cdot\frac{1}{3}x^3+\frac{2a^5}{5}x\right)\Bigg|_{x=-a}^{x=a}\\
&=\frac{3\rho_0}{16a^4\rho_0}\left(2a\cdot\frac{2}{5}a^5+\frac{4a^3}{3}\cdot\frac{2a^3}{3}+\frac{2a^5}{5}\cdot 2a\right)\\
&=\frac{3}{16 a^4}\cdot \frac{112}{45}a^6=\frac{7}{15}a^2.
\end{align*}
By symmetry, \(\bar{x}=0\) , \(\bar{y}=0\) .
(3) The moment of inertia is
\begin{align*}
I_0&=\iiint_\Omega \rho_0\left(x^2+y^2\right)dV=\rho_0\iiint_\Omega\left(x^2+y^2\right)dV\\
&=\rho_0\int_{-a}^a\!\!\int_{-a}^a\!\!\int_0^{x^2+y^2}\left(x^2+y^2\right)\,dz\,dy\,dx\\
&=\rho_0\int_{-a}^a\!\!\int_{-a}^a\left(x^2+y^2\right)^2\,dy\,dx\\
&=\rho_0\cdot \frac{112}{45}a^6=\frac{112}{45}a^6\rho_0.
\end{align*}
Note that in the computation above we reused the intermediate result in (2) that
$$\int_{-a}^a\!\!\int_{-a}^a\left(x^2+y^2\right)^2\,dy\,dx=\frac{112}{45}a^6.$$
Problem 7. Consider a Cartesian coordinate system with origin at the geometric center of the cylinder, with \(z\) -axis aligned with the axis of symmetry. Then the cylinder occupies the following region in \(\mathbb{R}^3\) :
$$\Omega = \left\{\left(x,y,z\right) \mid x^2+y^2\leq a^2, -\frac{h}2\leq z\leq \frac{h}{2}\right\}.$$
The desired moment of inertia is with respect to the \(z\) -axis. Therefore,
\begin{align*}
I_0&=\iiint_{\Omega}\left(x^2+y^2\right)dV=\int_{-\frac{h}{2}}^{\frac{h}{2}}\iint_{\left\{\left(x,y\right)\mid x^2+y^2\leq a^2\right\}}\left(x^2+y^2\right)dA\,dz\\
&=\int_{-\frac{h}{2}}^{\frac{h}{2}}\int_0^{2\pi}\int_{0}^{a}r^2\cdot rdr\,d\theta\,dz=\int_{-\frac{h}{2}}^{\frac{h}{2}}\int_0^{2\pi}\frac{a^4}{4}\,d\theta\,dz\\
&=\int_{-\frac{h}{2}}^{\frac{h}{2}}2\pi\cdot \frac{a^4}{4}\,dz=\frac{\pi a^4}{2}h.
\end{align*}
Problem 8. Note that the ball is symmetric so it doesn't matter which direction you pick to slice. Let's try slicing along the \(z\) -axis. The bounds in \(z\) is from \(-1\) to \(1\) . For each fixed \(z\) , the slice of the ball has equation \(x^2+y^2\leq 1-z^2\) , i.e. it is a disk in the \(xy\) -plane of radius \(\sqrt{1-z^2}\) . Thus
\begin{align*}
\mathrm{Vol}\left(B\right)&=\iiint_BdV=\int_{-1}^1\iint_{\left\{\left(x,y\right)\mid x^2+y^2\leq 1-z^2\right\}}\,dA \,dz\\
&=\int_{-1}^1\mathrm{Area}\left(\left\{\left(x,y\right)\mid x^2+y^2\leq 1-z^2\right\}\right)\,dz\\
&=\int_{-1}^1\pi \left(1-z^2\right)\,dz=\pi\left(z-\frac{1}{3}z^3\right)\Bigg|_{z=-1}^{z=1}\\
&=\pi\left(\frac{2}{3}-\left(-\frac{2}{3}\right)\right)=\frac{4}{3}\pi.
\end{align*}